概率论上,设一个随机变量X,求得其分布函数F(x),另有一随机变量Y,若Y = F(X),那么Y满足均匀分布。所以直方图均衡化,就是把像素值X,求得其累计直方图F(x)的映射,将这个映射用到X上,得到均匀分布的Y,只不过这时Y的分布范围是在【0,1】之间的小数,要先拉伸其范围到整个灰度区间,再量化为整数,所以就出现了量化的误差,导致得到的新的分布并非严格均匀分布
相关文章
Inside ASP.NET 2.0 – Controls Model
Inside ASP.NET 2.0 – Controls Model 文/黄忠成 (原文刊登于Run! PC) 读者基础需求:了解ASP.NET 控件设计技巧參考书目:深入剖析ASP.NET 组件设计(碁峯)、Developing ASP.NET Server Controls And Components(MS Press) Controls Model 的变革如你所知…
SRGAN 阅读笔记
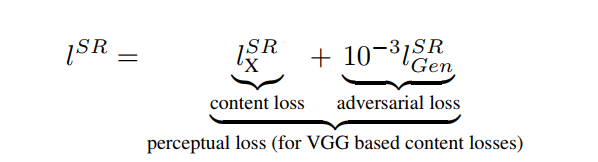
PSNR高的不一定更清晰:因此需要采取MSE之外的loss来衡量,GAN提供的Discriminator是很好的选择loss由两部分组成,一部分是GAN的adversarial loss,一部分是content loss(VGG的前几层)bilinear、bicub…
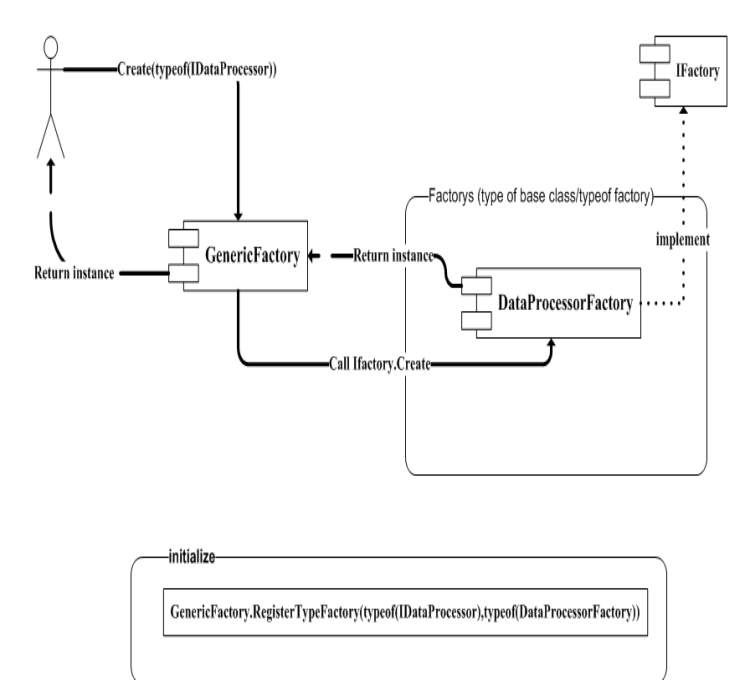
Inside ObjectBuilder Part1
Object Builder Application Block文/黃忠成2006/9/21一、IoC 簡介IoC的全名是『Inversion of Control』,字面上的意思是『控制反轉』,要了解這個名詞的真正含意,得從『控制』這個詞切入。一般來說,當設計師撰寫一個Console程式時…
ESRGAN阅读笔记
从三个地方入手修改了SRGAN: 网络结构adversarial lossperceptual loss 网络结构主要是引入了RRDB的结构,并且去掉了BN层,使用residual scaling和smaller initialization,就是residual在加的时候乘一个小于1的系数,在w…
Inside ObjectBuilder Part 2
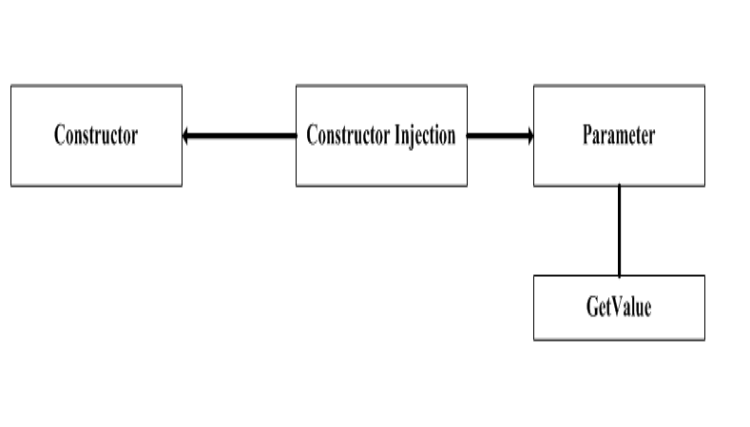
Object Builder Application Block文/黃忠成2006/9/21 三、ObjectBuilder Application BlockObjectBuilder一開始出現於Microsoft所提出的Composite UI Application Block,主司物件的建立及釋放工作,她實現了本文前面所提及的Dependency Injection概念&a…
嵌入式系统学习笔记(1)——概述、发展历史
TTL电平高电平为5V低电平为0V,计算机串口使用RS232电平,高电平为-12V低电平为12V,所以使用TTL电平的单片机和计算机通讯时需要通过电平转换芯片max23251单片机是对8051单片机衍生系列的统称,STC是其中一种,STC是公司的…
Inside ObjectBuilder Part 4
ObjectBuilderApplicationBlock文/黄忠成2006/9/21八、ObjectBuilder实务8-1、ObjectBuilderWithConfiguration截至目前为止,本文一直以程序方式来配置ObjectBuidler建立对象所需的各种对象,但在实务上,这些动作应该是交由配置文件来负责&…